The Law Of Identity

The Pattern of Logical Rules

In analyzing logical rules, you come to see a strange pattern. The rules are so intertwined that what explains a rule is always another rule, and what explains that other rule is always a rule other than itself. The structure is quite recursive and regressive, meaning that a logical rule contains within itself the whole system of rules, there's no assertion without its conditions. But how can the word or expression imply or presuppose the whole structure? We have here the law of identity, defined as (A ≡ A), "What is the same as something is that thing itself". This law is usually taken to refer to external identities; but what it really points to, the 'identical' itself, is that which different things have in common. We noted this in two instances, to say p is true and -p is false, are values of the same underlying reality, the context which relates them to each other, as A. Alexander puts it

"Two things are alike only if they are different, and different if they are identical" (Space, Time & Diety, p247).

Thus an identical proposition never pertains to the elements of the proposition, but to the underlying 'context', that which they have in common, the ground on which both stand, and on which their union depends.

Identity and Quantum Mechanics

If we ask what is it that can be said to be the 'case' with anything whatsoever?, we find that it's the fact that they can be held to be true or false, i.e., their logical value, that they fall within the logical structure of 'possibility and validity'. Here we express identity in our orientation to the basis of some concept or term. By approximation, what in quantum mechanics is called superposition, is really what the law of identity states, and is really the best expression of this principle, because identity is not something we arrive at, but a condition from which we begin. It's something we already assume in things we interact with at any level, and the most precise and true of those levels is the level that represents this assumption as a precondition, because in this sense it would be acknowledging its place in the order of mental acts.

Thus Identity is the underlying structure, the systematic basis of something. Or it can be thought of this way: that identity is the minimal requirement or critical mass for a relation with something; the sine qua non of some process. You can see that this is always the case, whatever the case may be; judgement may say that it's a tree, a door, a skyline, but the condition logic proscribes survives in each case making the judgement expedient.

Non-Contradiction and Identity

The fact that identity rests upon non-contradictory grounds means that the word can assume any form or shape whatsoever, but remain essentially tied to that scheme in which it's the continued object of analysis. Thus given a proposition p, identity asserts the context in which p is meaningful, this can range from the specific scheme in which p appears, e.g., the exportation formula p → (q ^ r), or it can point to the system of propositional calculus that is the ground of p. Whatever the case may be, it posits the domain of relation rather than the element of relation.

Rules of Replacement

Identity, just like the law of excluded middle, and non-contradiction, is composed of rules of replacement. We find here the rules of commutativity (used heavily in algebra) which states (p ^ q) = (q ^ p) (the order of the operands does not affect the result of the operation), and material implication (which refers to the relationship between two propositions where one proposition implies another), e.g., (p → q).

How are these two rules linked?

This is shown in the symbolic expression, the conjunction of any two terms, p and q in particular already relies on implication as a means of explaining the terms related. That p to be related to q, is given prior, and independent from the fact that we can explain or assert it, the relation; but logic wants to explain this prior connection: Here it uses material implication; that there's a relation between two things means that one is related to the other, and the other is related to the one, this explanation automatically gives us the rule of commutativity, but it gives it as a vehicle of explaining the relation of implication between the terms.

In relation to the law of identity as we've defined it, we can see how one instance of implication reveals all requisite orders of the terms related, and how inversely the order itself contains/reveals the particular relation of the terms to one another. We see here how in one stroke, these two rules relate to each other. At every level of analysis, the same structural conditions arise, the same schematism is reintroduced, and the order of rules remain applicable at every rendition and instance of the term.

We see thus how identity relates to the conventional sense of that word, only here its necessary form is more pronounce. We also see what Kant means by the statement ("The conditions of the possibility of experience in general are likewise the conditions of the possibility of the objects of experience."), for commutativity here gives us the conditions of the possibility of some relation, of which implication is the demonstration. The commutative relation grounds the implication, and implication arises from the commutative order.

Absorption and Identity

A closer look will show you how identity relies on the other rules; it relies for instance on 'absorption', for the introduction of the same conditions requires that these conditions be absorbed, and it relies on tautology, in order that the conditions be valid whether stated or simply held possible. But identity is not expository, it does not explain what goes into the claim, it only grounds or bases, it says that there's no instance of the system that's baseless. Whitehead uses the expression 'occasions' to approximate this relation, but our mind registers such occasions, or instances of identity by notions like 'basis', 'ground', 'fundamental'.

Whitehead's Occasions

But an occasion of the sort is only 'occasional' because there's a ground for it; thus Whitehead would add to occasion the expression concrescence, and together, these phenomena explain how what he calls actual occasions arise. Think of how each drop of saliva contains the genetic/biochemical information that reflects its entire biological lineage, each single act of logical inference necessarily embeds or instantiates the entire system of logical rules that makes inference possible. The same act thing that brings us the occasions, is what's occasioned.

Concrescence is the process by which many things come together to form one new actual thing. It's like how multiple experiences/feelings combine to create one moment of experience.
Actual Occasions are the fundamental units or "drops" of reality/experience. They're the basic building blocks of everything that exists. Think of them as moments of experience or events rather than enduring substances.
Occasions more broadly refers to the general process or happening of these experiential moments. While actual occasions are the specific, concrete instances, occasions refers to the ongoing process of their occurrence.

The Logical basis of Whithead's concept

See how the implication ‘occasions’ the commutative order, and how the commutative order ‘grounds’ the implication. When we explain what goes on in a commutative relation, we always go passed commutation, we used ‘material implication’ to explain how x relates to y, and how y relates to x. This is commutative by ‘inference’, but ‘implication’ by analysis. This is the same dynamic which Whitehead, a mathematical logician deploys in his ‘process philosophy’ concepts here. They explain the ‘interplay’ of a domain/ground, with that process which realizes it instantly. ‘Fundamental drops’ of ‘reality’; note the contrast between the very large and the very ‘small’, an aptly mereological relation. Think of the ‘occasion’ as an implicational procedure, and that which it occasions, as ‘reality’ at large. It will immediately occur to you that this, indeed, is how the universe articulates itself from moment to moment.

Application to Quranic Analysis

Thus when analyzing a Quranic term, this rule maintains that the term is based or grounded in the system of logic in which it's held as an analytic entity. But also that it's based or grounded in the Quran, as the system in which the word is found; this shows that identity has a subjective pole, the system of logic, employed by the analyst, and an objective pole, the environment or domain in which the term naturally occurs. But there's a relativistic side to what may ground some occasion of a term, and this is decided by the context and the factors that are in play, Quran-wise this may be the chapter in which the word occurs, or 'trans-contextual', a topic that spans a number of chapters, or the whole Quran.

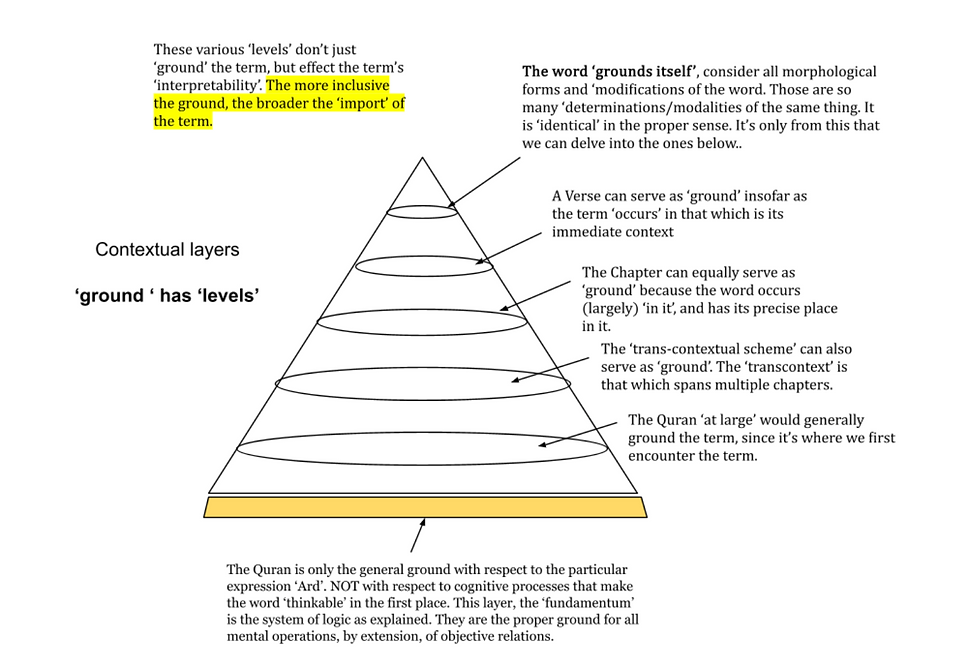
If we're talking the system of logic, then we may start by seeing what rules happen to be occasioned, say, tautology, then make an inference to non-contradiction as the relative ground, if contraposition, then we may infer the law of excluded middle as the ground, if modus ponens, then the rules of inference as the ground, and so on. There's a relative ground, for any relative occasion, and that ground is usually some class or set to which it immediately and most proximately relates. But suffices to know that the law of identity is embodied in this capacity to continually refer to this ground, and in the characteristically commutative and implicational structure in which the occasion is related to its ground. Thus, as universal quantification confirms, the same objective relations that reveal for us the identity of some term, are the same as those which we apply to identify the term.

Identity is essential because it emphasizes the systematic basis of any occasion, as from it, we can deduce the specific import of any rule.

Systematicity & Logical Regression

Systematicity as defined in this paper:

Systematicity and a Categorical Theory of Cognitive Architecture: Universal Construction in Context

We can regress to any other logical function/rule by a definite, consistent sequence, or from a mere conjunction, we can derive or obtain, for example, the rule of distributivity; that, insofar as a conjunction necessitates at least two terms, distributivity makes this possible by formally distributing the terms to both sides of the equation which conjunction mediates. Or if we so choose, we can derive from distributivity the rule of associativity by adding a predicand or subject to the distribution; thus we can place as the right argument of an algebraic equation the number 4 and the left argument, the number 5, and infer that this distribution of terms was conducted by way of their sum, the number 9, and 9 being that number through which this association of number is made possible. We've here derived an associative rule from a distributive function, and showed that these two rules are related a priori. We can do this with any rule of logic, and demonstrate the regression by a definite chain of deductions.

The distributive law in propositional logic has two forms:

p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r) p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)

In words:

Conjunction distributes over disjunction
Disjunction distributes over conjunction

It's similar to how multiplication distributes over addition in math: a × (b + c) = (a × b) + (a × c)

What does this even mean?

It depends on ‘identity’. Much like p grounds its ‘truth’ and ‘falsehood’, we can reverse this to say that p, the ‘ground’ is ‘distributed’ across the ‘truth-false’ propositional ‘spectrum’. It’s ‘distributive’ in that p occurs as true and as false, or, as truth or as false. This obviously entails that the ‘distributed’ element is ‘distributed’ throughout every domain or rule to which the basic condition set up by non-contradiction applies.

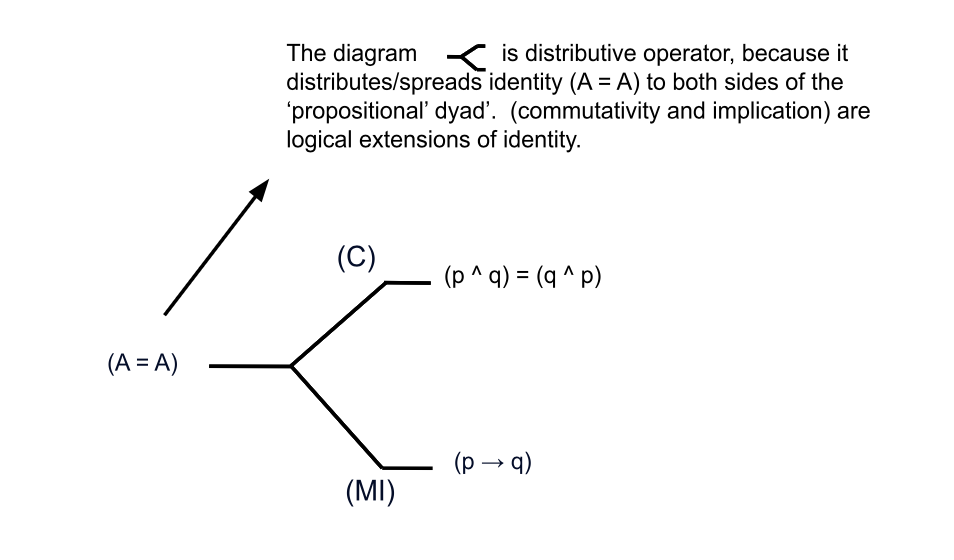
We can understand by this that the division or 'reduction' of the laws of thought into 'rules of replacement' occurs in a distributive manner. The rules of commutativity and material implication are nested within the law of identity, or, to put it differently, the law of identity is presupposed in the conjunction of these two rules. You can think of it as the 'empirical' representation or 'playing out' or 'unfolding' of the law of identity. Have a look at the diagram below:

Sufficient Reason (PSR)

What we're demonstrating in the previous section, particularly where we showed the regression from one rule/law to another, is not the law of identity, but another rule, a rule that's not often counted among the three fundamental 'laws' of thought, (PNC, LEM, IDN): a rule without which, we cannot even begin to think about them. Let's start with examples from philosophy,

When I think about a chiliagon [pronounced kill-ee-a-gon], that is, a polygon with a thousand equal sides, I don’t always think about the nature of a side, or of equality, or of thousandfoldedness. . . .; in place of such thoughts, in my mind I use the words ‘side’, ‘equal’ and ‘thousand’. This kind of thinking is found in algebra, in arithmetic, and indeed almost everywhere. I call it blind or symbolic thinking. When a notion is very complex, we can’t bear in mind all of its component notions at the same time, ·and this forces us into symbolic thinking. When we can ·keep them all in mind at once·, we have knowledge of the kind I call intuitive."

Leibniz 'Meditations On Knowledge, Truth and Ideas' 1684 (Link)

"In throwing dice we do not know the fine details of the motion of our hands which determine the fall of the dice and therefore we say that the probability for throwing a special number is just one in six"

W.Heishenberg 'Physics and Philosophy' (p12) link

"There, in our minds, we find habits which are dispositions of response to situations of a certain kind. On each occasion the response, let it be an act of will like telling the truth when we are asked a question, or the simpler instinctive response to a perception like holding our hands to catch a ball which is thrown to us—on each occasion the response is particular or rather individual, but it obeys a plan or uniform method. It varies on each occasion by modifications particular to that instance. It may be swift or slow, eager or reluctant, slight or intense ; the hands move to one side or another with nicely adapted changes of direction according to the motion of the ball"

S.Alexander 'Space, Time & Diety, (p211) ink

In using any rule of logic, we always, as the law of identity informs, rely and fall back on all other rules of logic; this means that a rule is only a certain way of grouping the others, and that each rule varies in the manner of these configurations (which calls to mind the rules of contraposition and exportation, as here it's shown how the system is expressed from the standpoint of one of its particulars). Now the system's 'self-relating' or 'self-explaining' capacity is what we're here concerned with. This is what's termed the principle of sufficient reason (PSR).

Example from Arithmetic

How do you get the number 6 using the four basic arithmetic operations? There are several if not 'infinite' ways of doing it.

Here are some:

3 + 3 = 6,
2 + 4 = 6
1 + 2 + 3 = 6,
2 + 4 = 6
10 − 4 = 6,
8 − 2 = 6

You can see that each operation is a 'sufficient' way of obtaining 6, sufficient in that it involves a deductive (or inductive) chain of operations whose basis is the self-same system of numbers! This 'systematicity' or 'systematic' unity is precisely what makes the deduction, and the 'location' or 'triangulation' of 6, possible. But, see that this application proves more than anything, the systematicity of the field of application, the unity of the terms under that one coherent framework.

In logic, this is expressed using 'negation'; this isn't immediately obvious from something like -p or -q; as it requires a systematic grasp of these functions and how they relate to one another; we need to know how falsehood qualifies truth, and truth, falsehood, how deductions are possible, given a set of correlated terms. We negate p or any other variable, only as a reference to some underlying context; I negate so as to defer an explanation or proof; I don't know how this value is obtained, so I negate it to say that there's an explanation for it, but an explanation whose precise details I do not possess.

The Interdependence of Logical Rules

Put it this way, that without PSR no deduction is possible, or that without IDN, no definitions are possible, or that without PNC and LEM, no scheme on the basis of which something could be defined or inferred is possible; is an example of the schematic application of sufficient reason, in showing the intimacy of the relations among the rules of logic or their objects, for PSR is what allows you to glean this interdependence in the first place!, and you use it in determining how one thing depends upon another; in determining contingencies, consequences, implications, presuppositions, because, in each of these cases you are explaining some system through certain 'contextual links', you find some unifying principle → here identity, as a criterion, through which to understand how a thing relates to another schematically.

This is because what PSR primarily explains, isn't the content of judgement (Leibniz's chiliagon, or Alexander's ball, or Heisenberg's dice) but how the laws of identity, of excluded middle, and non-contradiction specifically cohere, and in proving the reconstructability of the rules out of each other, and their relatability and contingency, PSR renders this a faculty applicable to any external system, but only because the modularity of these external systems will be based on the modularity of these core 'laws of thought'.

Rules of Replacement in PSR

PSR isn't unlike the other three laws in being composed of other rules of replacement; here we find the rules of transposition and associativity.

Associativity

Formal Expression:

For Conjunction: (p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
For Disjunction: (p ∨ q) ∨ r ≡ p ∨ (q ∨ r)

Means operations can be regrouped without changing the result - (p ∧ q) ∧ r is equivalent to p ∧ (q ∧ r). The order of grouping doesn't matter; you get the same truth value regardless of how you bracket the expressions. It applies to both conjunction (AND) and disjunction (OR) operations.

Transposition

Formal Expression:

(p → q) ≡ (~q → ~p)
Where '→' represents implication and '~' represents negation

This rule reveals a deep symmetry in logical relationships - it shows that when two things are necessarily connected, this connection works both forwards and backwards. It's not just a rule about switching terms around; it demonstrates how logical necessity contains within itself its own reverse image. It denotes a ‘homeomorphic relation’ (In mathematics, a homeomorphism is a one-to-one mapping between two topological spaces that is continuous in both directions. Britannica) between the elements of a proposition p and q (which can be extended to their negations), These two elements are simply the higher order truth (or falsehood) and their lower order ‘image’.

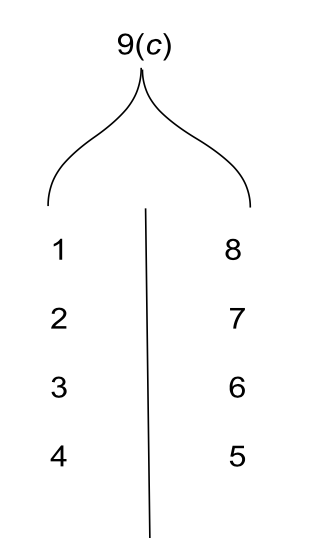
This last point is important. E.g in a relation between 4 and 5 in the equation (4 + 5), transposition isn’t the openness of 4 to 5 and backwards, so much as the openness of their sum (9) - the very condition on which the possibility of this equation holds) - to each of them. To the left is a more precise mathematical example of this concept which holds everywhere.

Here you can speak of ‘translatory’ process between the sum and each derivative of the sum, the interrelation between aspects of one thing stems from the openness and continuous relatability of the elements to one another, a condition made possible by that in which these relations and the elements related naturally occur, or fall under. For example, the chemical mixing of two compounds, does not only result in a new compound that combines them both, but in the combining of the minute elements that make them up, thus to combine the two is to combine all their composite elements, it’s this relatability and synthesis among the smaller composites that make the new larger synthetic compound possible. This is what transposition denotes.

This is different from associativity, but remains essential to it, and inexpressible without it. Transposition requires a organizing, constructive principle to provide the essential mechanism of relations and relatability, associativity likewise requires a transformative, deconstructive principle by which to express and demonstrate the associative processes

Comparing 'similar' rules of replacement

Associativity and Exportation

Associativity resembles exportation in a certain respect; exportation relates signs or modes to some general object, it allows us to think of something through something else, like, you can think of the past only in the present, or the whole only through some part, these are exportation statements, (We've explained what we mean by 'object' in part 3: we said that the object in the logical sense is never as concrete as the 'instance' that refers to it, but a 'possible object', an object in the inductive sense, an 'index', something that could only be approximated but never really 'attained'.

In Associativity the scheme is reversed, you think instead of how you can wield some concept and give examples or cases of it, thus the part becomes a predicate or example of the concept which in exportation appears as the objective; it denotes the principle or 'rule' by means of which a certain scheme is possible; e.g., in enumeration or thinking of relations between red, yellow and orange, associativity would denote the concept 'color' as their associative or organizing principle; even when mixing two things that don't seem to belong to one another; the associative or organizing principle is their possible sum → insofar as it's possible to relate the two objects in the first place. We can extend this to any 'conjuntion', disjunction, 'implication', addition, multiplication, division: insofar as all of these operations start from and 'rest upon' the 'relation' of two or more terms, numbers, objects etc.., associativity would be that relation concept/principle, or that through which the relation between the two terms/objects is possible. This is indicated by the symbolic formula (p ^ q) ^ r = p ^ (q ^ r)

While exportation (→ r) shows how a conjunction becomes determined through an act of relating terms (like actively adding 3 and 3), associativity (^ r) reveals that this relation was already possible within the system itself. In other words, exportation demonstrates how 3 + 3 leads to a determination ('I am adding these numbers'), but associativity shows that this addition was already inherent as a possibility within the sum 6. The sum 6 already contained within it the potential for being expressed as 3 + 3, before any actual addition took place. Thus, associativity doesn't imply a determination of conjunction (p → (q ^ r)) but rather shows that such relations are already given within the system's structure. The logical formula expresses the 'givenness' of the addition 3 + 3, by means of the 'conjunction' operator (^) which says that the Conjunction implies that the two propositions are both true at the same time or in the same context: That', the resulting proposition is true only if both individual propositions are true, i.e that the relation is given prior to the assertion. Compare this to the exported (->r) which is the assertion itself!.

This is why a conjunction is used in place of implication in the associative formula, for, as we noted in relation to the law of identity, conjunction expresses a formal relation as opposed to implication (an immediate implication, that is, the assertion that there's a conjunction) which explains how one term is related to the other. The difference in the use of these operators reflects the difference between these two rules; we use a material implication to express mediation → how terms relate to each other, and a conjunction to express 'prior-ness', how the terms are already necessarily related to each other, and just as exportation shows how we come to choose our terms, so does associativity indicate the concept in terms of which a certain relation is formed; or that the related is already nested in some concept. The selective nature of each determination is clearly present in both cases.

The same relation is found between transposition and contraposition; despite being symbolically identical, there's a crucial difference.

The Relation of Transposition to Contraposition

Just as Contraposition relates the continued possibility of inference, to generalize, so does transposition allow for the possibility, from the standpoint of the same system, to specify, to 'introduce' and instantiate, namely, the same instance, from which contraposition makes its generalizations.

The two are functionally the same, but opposite in their tendencies; the continued possibility of inference and the continued possibility of reference, are consistent with the rules with which we find them already associated; the continued possibility of reference, transposition, is consistent with the associative rule in the sense that both embody rules or principles in relation to which objects or data are examples; just as in contraposition we have a panoramic depiction of the whole, from the standpoint of a variable, undefined, general instance, so in transposition, we have the continuous possibility of instantiation or representability of the instance from the standpoint of the system at large. In transposition, the whole is our premise and the instance our objective, whereas in contraposition, the instance is our premise and the whole, our objective. They explain the same scheme from two different directions.

The import of the law of sufficient Reason to the Quran

Reflect on what we said regarding the applicability of the preceding three laws to the Quran; how non-contradiction restricts us to the conditions of possibility-validity of the given term, how these 'analytic' functions are grounded in, and proceed from the unity of term itself; and how we're able to determine these functions -> the term's possibility and/or validity in any given instance, or let's say there's what's immediately the case, say a specific morphological form of the word, then there's 'what could be'. Our oscillation between these conditions is made possible through the law of excluded middle. Do you see how these laws depend upon one another through and through?, is this not explainable negatively?, by saying how 'identity' is NOT possible outside the context of non-contradiction, NOR is non-contradiction without a unifying element/term, Identity. NIETHER are any of the preceding condition possible without being 'determined' -> Excluded middle. This 'mode' I enter in, in which I'm able to 'glean' these interdependencies is precisely the law of sufficient Reason!

These laws, when applied to a Quranic term determine the conditions under which alone, we can analyse it and derive all that it 'means. They thus govern and determine 'structural conditions', or analytic/regulative guidelines according to which, any term/concept can be approach. But to clarify, the rules, when applied, are applied 'determinately' or intentionally, they are not applied accidently, as in, as things which naturally follow - though they do - from the principle of 'understanding' a term 'in-terms' of itself'. There are nuances which can only be 'accounted for', that is, 'intended'. The law of suffecient reason is what would permit us to 'ambulate' as it were, between the different structural conditions as applied to the a term. But the 'rigor' which these laws provide, extend to the objective conditions of the term itself -> as it occurs in the Quran.

"To compare, blend, combine, and arrange the various meanings, morphological expressions, and contexts in which the term is expressed is as much a function of these laws as are the basic logical conditions from which we generally proceed. We'll delve into this and show clearer examples in the articles to come, but suffice it to know that what the method espoused in these four articles establishes for us is simply the possibility of a 'guided' analysis of any given term. No longer are we to proceed 'blind'; instead, we have 'programs' by which to effect a targeted and almost 'computational' analysis of any given term."

Hermeneutics: Applying Mathematical Logic To The Quran (Part 4)